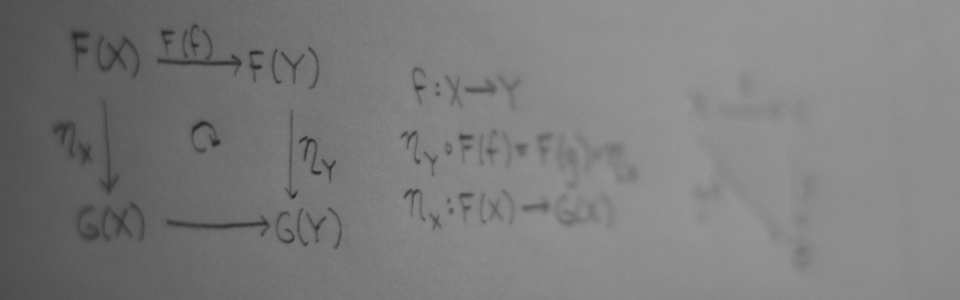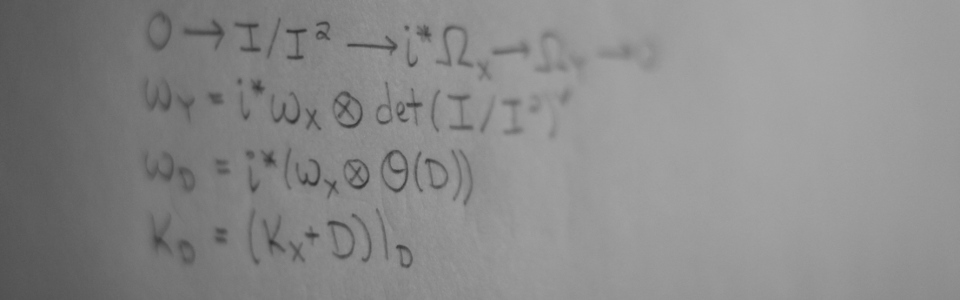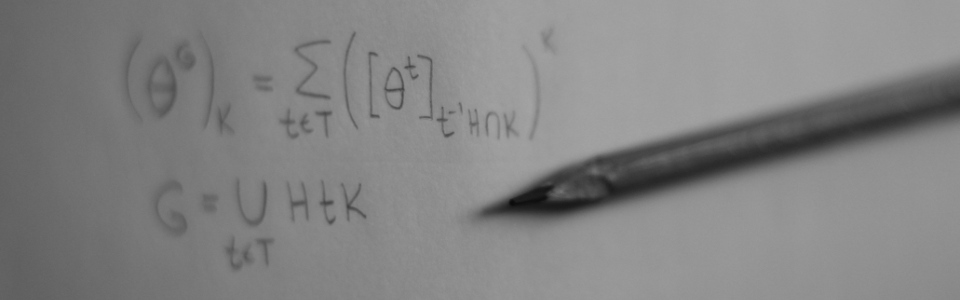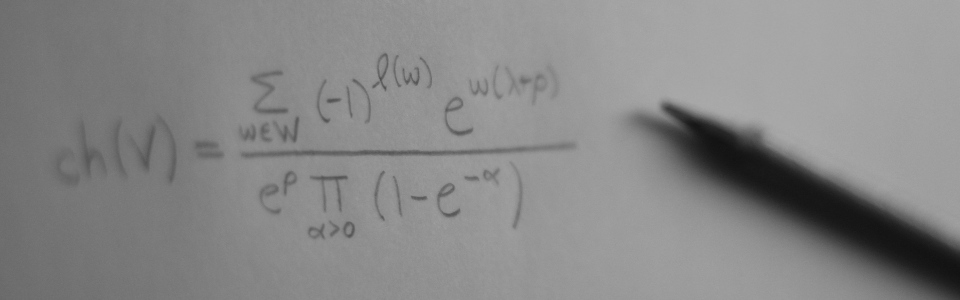Ottawa-Carleton joint algebra seminar (Fall 2016)

Kirwan surjectivity in real symplectic geometry and moduli spaces of vector bundles over a real curve

Kirwan surjectivity in real symplectic geometry and moduli spaces of vector bundles over a real curve

Abstract: In the early 80s, Kirwan proved a relationship between the equivariant cohomology of a Hamiltonian action on a symplectic manifold, and the cohomology of its symplectic quotient. I present an version of this relationship for symplectic manifolds equipped with an anti-symplectic involution, relating the cohomology of corresponding fixed point Lagrangian submanifolds. I then apply this result to study the topology of moduli spaces of vector bundles and Higgs bundles over a real algebraic curve, in the style of Atiyah-Bott and Hitchin.
 

The Gelfand-Kirillov conjecture and its analogues for finite W-algebras

The Gelfand-Kirillov conjecture and its analogues for finite W-algebras

Abstract: The original GK conjecture for a simple Lie algebra g states that the field of fractions of U(g) is a Weyl skew field over its central subfield. It holds in type A, fails in types B, D, E, F₄, and is wide open in types C and G₂. Since the finite W-algebras U(g,e) share with U(g) many ring-theoretic features, it is natural to ask for which nilpotent elements e in g the skew field of fractions of U(g,e) is a Weyl skew field over the centre. In my talk I will explain that this question leads to interesting problems of birational algebraic geometry.
 

p-group actions on smooth projective varieties

p-group actions on smooth projective varieties

Abstract: I will discuss how the geometry of an algebraic variety restricts the possible p-group actions on it, especially concerning fixed points.
 

Smooth Schubert varieties of affine type

Smooth Schubert varieties of affine type

Abstract: A natural question about Schubert varieties is: when is a Schubert variety smooth? In finite type, this question is completely solved. Not only can we recognize smooth Schubert varieties using pattern avoidance, but we can explicitly construct all smooth Schubert varieties as iterated fibre bundles starting from a short list of known manifolds.
Much less is known about smooth Schubert varieties of affine type. In this talk, I will discuss joint work with Ed Richmond in which we show that everything we know about finite type can be extended to affine type A. In particular, we show that every smooth Schubert variety of affine type A is an iterated fibre bundle of Grassmannians. I will also highlight some examples showing that interesting things can happen in affine type, including joint work with Lakshmibai and Ravikumar showing that the cotangent bundle to a cominuscule Grassmannian can be embedded in a smooth Schubert variety of an affine two-step partial flag variety.
 

Simple Lie algebra modules that are finitely generated over a Cartan subalgebra

Simple Lie algebra modules that are finitely generated over a Cartan subalgebra

Abstract: The problem of classifying all modules over a complex simple Lie algebra is beyond reach. Nevertheless, some classes of modules are well understood, for example the Weight modules, Whittaker modules, and Gelfand-Zetlin modules. In this talk I discuss a class of infitite dimensional modules which are finitely generated when restricted to a Cartan subalgebra. In particular I will show some results about the classification of modules whose restriction to the Cartan is free of rank one, and their connection coherent families.
 

On the cohomology ring of closed orientable Lagrangian submanifolds with vanishing Floer homology

On the cohomology ring of closed orientable Lagrangian submanifolds with vanishing Floer homology

Abstract: I will give new restrictions on the topology of certain Lagrangian 3-manifolds whose Lagrangian Floer homology vanishes and give applications to open Gromov-Witten invariants. I will provide the necessary background from symplectic geometry.
 

Commuting involution graph of linear groups

Commuting involution graph of linear groups

Abstract: Let G be a group and X a subset of G. The commuting graph of G on X is the graph with the vertex set X in which two distinct vertices are connected by an edge if they commute. When X is a conjugacy class of involutions, the corresponding graph is called the commuting involution graph. In this talk, we will discuss the diameter of the commuting involution graphs of linear groups over an arbitrary field. In particular, we will provide the diameters of general linear groups and certain projective linear groups. This talk is based on joint work with Changhyouk Han.
 

Differential algebraic and linearly compact Lie algebras

Differential algebraic and linearly compact Lie algebras

Abstract: The main goal of the talk will be to explain the connection between differential affine Lie algebras, considered in the works of Cassidy, Kirillov, Ritt, and linearly compact Lie algebras, studied by Cartan, Guellemin, Weisfeller and many others. While the categories are different, the classification of their simple objects is quite similar. Namely, we will see how the well-known Cartan's classification of primitive Lie algebras can be used to describe simple differential affine Lie algebras. If time permits, I will also explain the relation of these algebras to conformal Lie algebras, introduced by Kac.
 

Dual filtered graphs

Dual filtered graphs

Abstract: Using the Hecke insertion algorithm of Buch-Kresh-Shimozono-Tamvakis-Yong, we define a K-theoretic analogue of Fomin's dual graded graphs called dual filtered graphs. The key formula in the definition is DU-UD=D+I. We discuss two main constructions of dual filtered graphs: the Mobius construction, which corresponds to natural insertion algorithms, and the Pieri construction, which is an algebraic construction. This is work with Pasha Pylyavskyy.
 

Galois and Cartan cohomology

Galois and Cartan cohomology

Abstract: Rational forms of an algebraic group G are defined in terms of Galois cohomology H¹(Gamma,G/Z). Over R real forms can also be understood in terms of their Cartan involution theta, which amounts to studying "Cartan cohomology" H¹(theta,G/Z). It turns out there is a canonical isomorphism H¹(Gamma,G)= H¹(theta,G). As applications we give short proofs of some basic results in Lie theory, including the Sekiguchi correspondence (of nilpotent orbits) and Matsuki duality of orbits on the flag manifold.
 

Classification of category J modules for divergence zero vector fields on a torus

Classification of category J modules for divergence zero vector fields on a torus

Abstract: We consider a category of modules that admit compatible actions of the commutative algebra of Laurent polynomials and the Lie algebra of divergence zero vector fields on a torus and have a weight decomposition with finite dimensional weight spaces. We classify indecomposable and irreducible modules in this category. This is joint work with Yuly Billig.
 

Lattice points, convex bodies and algebraic geometry

Lattice points, convex bodies and algebraic geometry

Abstract: I will start by discussing some basic facts about the semigroup of finite subsets of Zⁿ. This leads us to beautiful results in toric geometry (Bernstein-Kushnirenko theorem on the number of solutions of a system of polynomial equations). I will discuss generalizations to arbitrary varieties/graded algebras and theory of Newton-Okounkov bodies. Beside applications in study of divisors on varieties, this extension introduces stunning new tools and ideas in a number of other areas such local commutative algebra (Hilbert-Samuel multiplicity), symplectic geometry (moment map and integrable systems) and representation theory (flag varieties and Schubert calculus). For the most part the talk is accessible to anybody with just a basic knowledge of algebra and geometry.